朴素贝叶斯分类器

完整代码：https://github.com/JiaZhengJingXianSheng/Naive-Bayes-Classify

基础

贝叶斯分类的基础是概率推理，就是在各种条件的存在不确定，仅知其出现概率的情况下，如何完成推理和决策任务。 而朴素贝叶斯分类器是基于独立假设的，即假设样本每个特 征与其他特征都不相关。 朴素贝叶斯分类器依靠精确的自然概率模型，在有监督学习 的样本集中能获取得非常好的分类效果。

条件概率

假设A,B是两个随机变量，它们的联合概率 P(A=x,B=y) 是指 A=x和B=y同时 发生的概率。

如果A和B是两个随机变量，且 P(B)≠0 。那么B条件下，A 的条件概率为
$$
P(A|B)=\frac{P(A,B)}{P(B)}
$$
我们用Ω代表总样本空间，P(A|B)的隐含假设是，B确定要发生。当确定B发生时， 样本空间不再是Ω，而是缩小成B。我们在B样本空间中 寻找A发生的概率。

贝叶斯定理

贝叶斯定理 （Bayes theorem） ，是一种对属性集 X（现象，事件，特征向量）和类变量 Y（条件，原因，类）的概率关系建模的方法，是一种把类的先验知识和从数据中收集的新证据相结合的统计原理。

基础原理

$$
P(X|Y)P(Y)=P(X,Y)=P(Y|X)P(X)
$$

贝叶斯定理

$$
P(Y|X)=\frac{P(X|Y)P(X)}{P(X)}
$$

贝叶斯分类

利用贝叶斯公式来计算样本属于各类的后验概率 $P(w_i |x)$
$$
P(w_i|x)=\frac{P(x|w_i)P(w_i)}{P(x)}
$$
其中，x是特征向量， $w_i$ 是类标签。

先验概率： $P(w_i)$ 可以由大量的重复实验所获得的各类样本出 现的频率来近似获得，其基础是“大数定律”。

从测量中获得了样本的特征向量后，依照 $x和w_i$ 的组合确定似然函数 $P(x|w_i)$ ，再运用贝叶斯公式计算后验概率 $P(x|w_i)$ ，通过找出使后验概率 $P(x|w_i)$ 最大的类 $w_i$ ，对样本进行分类；

前提条件： 假设属性之间条件独立。

多分类问题

已知样本分为 m 类 $w_1,w_2,…,w_m$ ，各类的先验概 率 $P(w_1),P(w_2),…,P(w_m)$

核心步骤：

  1. 计算对应的各类条件概率 $P(x|w_k)$

  2. 求出对应的后验概率 $P(w_k|x)$ ，即M 个判别函数

  3. 寻找最大值：
    $$
    P(w_k|x) = P(w_k)P(x|w_k)=max{ P(w_j)P(x|w_j) } \qquad 1 \le j \le m
    $$

  4. 把x归于概率最大的那个类。

代码实现 - 手写数字识别

一、 准备工作

我们需要调用 sklearn.naive_bayes 下 GaussianNB 的包

GaussianNB 的定义如下

1
2
3
4
5
6
7
8
9
10
Examples
    --------
    >>> import numpy as np
    >>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
    >>> Y = np.array([1, 1, 1, 2, 2, 2])
    >>> from sklearn.naive_bayes import GaussianNB
    >>> clf = GaussianNB()
    >>> clf.fit(X, Y)
    GaussianNB()
    >>> print(clf.predict([[-0.8, -1]]))

可以看出是将image和对应的label 分别传入fit函数，而fit函数定义如下

1
2
3
4
5
6
7
8
9
10
11
def fit(self, X, y, sample_weight=None):
    """Fit Gaussian Naive Bayes according to X, y.

    Parameters
    ----------
    X : array-like of shape (n_samples, n_features)
        Training vectors, where `n_samples` is the number of samples
        and `n_features` is the number of features.

    y : array-like of shape (n_samples,)
        Target values.

这意味着我们必须把单个图片tensor全部转为一行，再把所有的图片拼接起来。

二、 具体实施

1.导入相关包

1
2
3
4
5
6
from sklearn.naive_bayes import GaussianNB
import matplotlib.pyplot as plt
import numpy as np
import torchvision
import torch
from torchvision import transforms

2. 设定相关参数

1
batch_size = 32

3. 下载数据集

1
2
3
4
train_data = torchvision.datasets.MNIST("data", train=True, download=True, transform=transforms.ToTensor())
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size, shuffle=True)
val_data = torchvision.datasets.MNIST("data", train=False, download=True, transform=transforms.ToTensor())
val_loader = torch.utils.data.DataLoader(val_data, batch_size=batch_size, shuffle=False)

这边我们使用pytorch下载并读取数据集，并转为tensor -> transform=transforms.ToTensor() 。

4. 数据预处理

MNIST数据集 包含 60000个训练样本和10000个测试样本 ，每张图片都是 28x28 像素。事实上，上面的数据集尺寸并不是我们想要的，以训练集距离我们的尺寸是 [60000/batch_size ， batch_size , 28 , 28 ] 的数据，我们要将其转换为 [60000, 28x28 ] 的形式。label的尺寸为60000行。

接下来我们定义预处理函数

1
2
3
4
5
6
7
8
9
10
11
12
def pretreatment(data, batch_size):
    image = []
    label = []
    for i in range(len(data)):
        x, y = next(iter(data))
        for ii in range(batch_size):
            image.append(x[ii].reshape(1, -1)[0].tolist())
            label.append(y[ii].item())

    image = np.array(image)
    label = np.array(label)
    return image, label

我们对每一个迭代出的 x，y 实际上是 batch_size张图片 ，我们遍历图片并将每张图片展平成一行。对于label我们只需要拿出他们的值即可，最终 转为numpy并返回 。

1
2
train_image, train_label = pretreatment(train_loader, batch_size)
val_image, val_label = pretreatment(val_loader, batch_size)

至此我们就可以得到所需格式的数据

5. 训练

1
classify = GaussianNB().fit(train_image, train_label)

训练相对容易，只需要将对应值传入即可。

6. 预测

1
predict_label = classify.predict(val_image)

调用predict函数并传入预测数据集即可得到预测结果

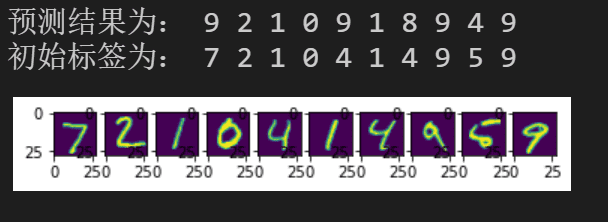
我们这边打印10张图片，并在前面打印预测结果。

1
2
3
4
5
6
7
8
9
10
11
plt.figure(1)
print("预测结果为：",end=" ")
for i in range(10):
    plt.subplot(1, 10, i + 1)
    plt.imshow(val_image[i].flatten().reshape(28, 28))
    print(predict_label[i], end=" ")

print("\n初始标签为：",end=" ")
for i in range(10):
    print(val_label[i],end=" ")
print()

7. 评估

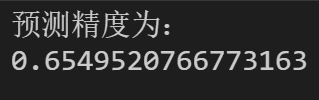
我们计算预测结果等于本身label的数量，除以总数即为预测精度。

1
2
3
4
5
6
sum=0
for i in range(len(val_loader)):
    if val_label[i] == predict_label[i]:
        sum += 1
print("预测精度为：")
print(sum/len(val_loader))