贝叶斯法则和机器人学

基础

在给定的初始预测下，我们就可以改进预测。

假设我们的初始预测（先验信息）是对汽车在道路上位置的估计，我们获得的是不太准确的卫星定位，我们可以根据汽车周边的数据和汽车移动方式的数据来改进我们的预测。

传感器

无人驾驶汽车主要使用以下三种传感器观察世界：

摄像头 ：可以拍摄视频，
光学雷达 ：是基于光学的传感器，
雷达：使用无线电波。

无人驾驶汽车也有许多 内部传感器 ，可以测量汽车行驶的速度和方向、车轮方向，甚至是车内温度！

举个栗子（😄）

假设我们的传感器探测到地形和汽车行驶的具体信息，如下：

这辆汽车可能在方圆半径 5 米的任何地方，
汽车正在爬坡行驶，
汽车左侧有棵树，
汽车车轮指向右边。
这条路是单行道

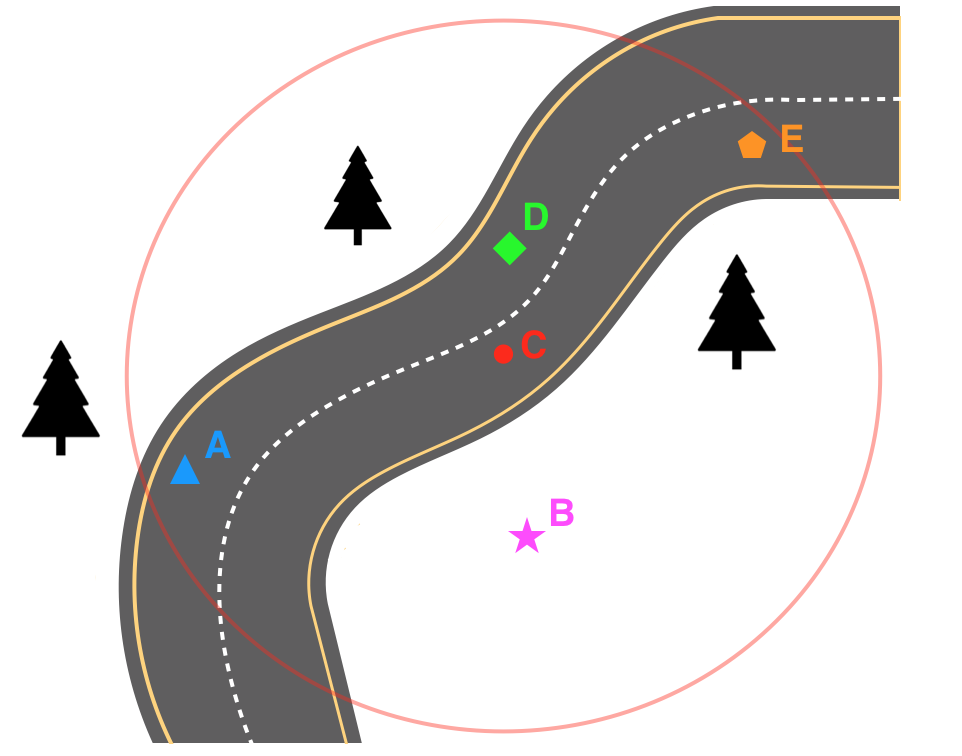
那么显而易见车在A位置的概率最大。

条件概率

基础

如果让我们估计一年之后的天气情况，这可以近似看作一个独立事件。相反估计一分钟后的天气，你得出的结果会因为现在的天气状况做出判断。

这种利用收集起来的数据得出概率估计就是条件概率。利用我们已知的信息，对未知信息做出更好的估计。

碰撞的概率 [练习区]

车辆1	左转	直行	右转
左转	0.5	0.25	0.1
直行	0.25	0.02	0.1
右转	0.1	0.1	0.01

上面显示的真值表列出了两辆车同时尝试移动，则两辆车在十字路口发生碰撞的概率。例如，如果车辆 1 直行，车辆 2 左转，则碰撞概率为 0.25。

举个栗子（😄）

你希望得出一辆汽车看见黄色的交通信号灯就停下来的概率是多少。

经验数据告诉你，一辆汽车在交通灯交叉路口停车的概率是 \(P(S) = 0.40\) 。
同时你了解到，基于经验数据，交通灯是黄色（而不是红色或绿色）的概率是 \(P(Y) = 0.10\) 。

已知 P(Y|S) = 0.12 ,如果交通信号灯为黄色，那么汽车停下的可能性为 \[ P(S|Y) = \frac {P(S,Y)}{P(Y)} = \frac {P(Y|S)P(S)} {P(Y)} = \frac {0.12*0.04} {0.10} = 0.48 \]

栗子2（😄）

在一条四车道的高速公路上，汽车行驶速度要么快，要么不快。快的汽车应该在最左边的车道。

在任何时候，都有 20% 的车辆在最左边的车道。
总体上，高速公路上有 40% 的车辆被归类为快速行驶。
在最左边车道的所有车辆中，90% 的车辆正在快速行驶。

如果汽车行驶速度很快，那么它位于最左边车道的概率为：

设最左边车道为事件A，快速行驶为事件B, P(A) = 0.2, P(B) = 0.4, P(B|A) = 0.9 \[ P(A|B) = \frac {P(A,B)} {P(B)} = \frac {P(A)P(B|A)} {P(B)} = \frac {0.2*0.9} {0.4} = 0.45 \]